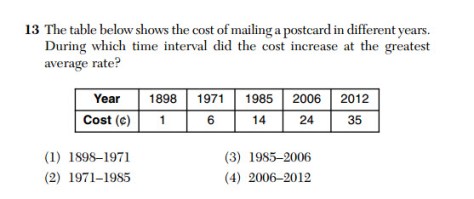
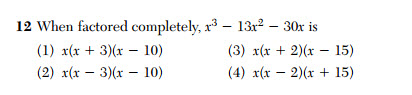Category Archives: test prep

Common Core Algebra I, medium, Regents, test prep

Get the Math and Get the Points Jan 2016 CC Algebra I Regents #14

Leave a comment

From the January 2016 Common Core Algebra I Regents

Jan 2016 Alg I 14

http://www.regentsprep.org/regents/math/algtrig/ate12/completesqlesson.htm

We can use the method of completing the square — see the link above
So far we have x^2 – 8x so we take 1/2 of -8 and square that to complete
(x –  4) (x – 4 ) giving x^2 – 8x + 16

trying answer (1) gives x^2 – 8x + 16 = 9  if we subtract 9 from each side we get:
x^2 – 8x + 7 = 0  close but no cigar

trying answer (2) gives x^2 – 8x + 16 = 23  if we subtract 23 from each side we get:
x^2 – 8x – 7 = 0  matches exactly!!!

OR

we can expand each answer and set it equal to zero to see which one matches the original whether on paper or on the TI-84
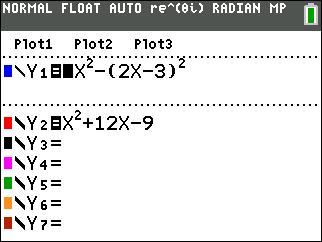
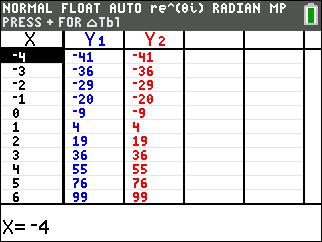
On the TI-84, set Y1 = x^2 – 8x – 7 and then set each answer choice to 0 and put into Y2 one by one
Try answer (1) by setting Y2 = (x – 4)^2 – 9, does it match Y1?
Try answer (2) by setting Y2 = (x – 4)^2 – 23, does it match Y1?  :)

 

 

Common Core Algebra I, medium, Regents, test prep

Get the Math and Get the Points CC Alg I Regents #13

Leave a comment

From the January 2016 Common Core Algebra I Regents:Jan 2016 Alg I 13

This is really a rate of change or slope question: (change in y) / (change in x)

For answer choice (1), it took 73 years to go up 5 cents not a lot of increase per year
For answer choice (2), 14-6 = 8 cents over 14 years (1985-1971)
For answer choice (3), 24 – 14 = 10 cents over 21 years (2006 – 1985)
For answer choice (4), 35 – 24 = 11 cents over only 6 years (2012 – 2006)

(We can see that the price change has been increasing by more cents as time goes on)
So which time interval had the most change per year?  Please see below

Jan 2016 Alg I 13

 

 

Common Core Algebra I, easy, Regents, test prep

Get the Math and Points Jan 2016 CC Alg I #12

Leave a comment

From the January 2016 Common Core Algebra I Regents

Jan 2016 Alg I 12

We can ‘do the FOIL’ or double distributive and/or we can use the TI-84 to find the equivalence to the given.  The choices look appealing as both 3 x 10 and 2 x 15 are factor pairs of 30.
To do  FOIL, we do the parentheses first in each case and then multiply by x and see if it matches the given x^3 – 13x ^2 -30x
(1) FOILing (x + 3) (x – 10) gives x^2 – 10x + 3x – 30 = x^2 -7x -30 and when  multiplied by x does not look like the original
(2) FOILing (x – 3) (x – 10) gives x^2 – 10x – 3x + 30 = x^2 -13x + 30 and when  multiplied by x does not look like the original
(3) FOILing  (x + 2) (x – 15) gives x^2 – 15x + 2x + 30 = x^2 -13x – 30 and when  multiplied by x looks familiar!
(4) FOILing (x – 2) (x + 15) gives x^2 + 15x – 2x – 30 = x^2 +13x – 30 and when  multiplied by x does not look like the original

Here is the TI-84 way — looking for equivalence :)
As you can see below answer choice (1) not a match

As you can see below answer choice (2) is also not equivalent:

Onto answer choice (3), see below: it’s a keeper –= this algebra is equivalent!!!!

 

 

Common Core Algebra I, hard, Regents, test prep

Get the Math and Points Jan 2016 CC Alg I #11

Leave a comment

from the January 2016 Common Core Algebra I Regents

Jan 2016 Alg I 11

No solving necessary!!  Just looking for the equation!!

Students need to remember how to find the area of a rectangle: length by width 

What was the original area of the patio?    The original area was 120 sq ft (10 x 12)
What is 50% more than 120?  Add 1/2 of 120 which is 60 making the new area  120 + 60 = 180 leaving answers (2) and (3).

Since we are adding x amount to each dimension 10 becomes 10 + x and 12 goes to 12 + x.
Those two multiplied together = 180 and voila there it is!

 

Common Core Algebra I, hard, Regents, test prep

Get the Math and Points Jan 2016 CC Alg I #10

Leave a comment

From the January 2016 Common Core Algebra I RegentsJan 2016 Alg I 10

Read this question carefully:  How much is 2 subtracted from 10?  10-2
Apply that to the problem above and we need to do:
5x^2 – (2x – 3)^2
We will need to FOIL (or double distribute) the (2x – 3)^2
(2x – 3) (2x – 3)
F:  (2x)(2x) = 4x^2
O: (-3)(2x) = -6x
I:  (-3)(2x) = -6x
L:  (-3)(-3) = 9
combine the like terms of -6x and -6x for -12x
4x^2 -12x +9  and subtract it from 5x^2 so it really looks like this:
5x^2 – (4x^2 – 12x +9) and the negative is distributed in the next line
5x^2 – 4x^2 + 12x – 9 then combine like terms and you have
x^2 + 12x – 9
match this up carefully — the answers look super similar

We could also use the TI-84 with Y1 for the original and Y2 for the answer choices
see below for answer choice (1)  this is NOT a match as the tables list different y values for the same x values and there are clearly 2 different graphs (red and blue)

Let’s try answer choice (2)  see below  also NOT matching up as the tables list different y values for the same x values and there are clearly 2 different graphs (red and blue)

ok onto answer choice (3) and look at the table for same values in Y1 and Y2!!!
Jan 2016 Alg I 10cJan 2016 Alg I 10c tableJan 2016 Alg I 10c graph

Unfortunately the TI-84 graph does not show the overlap of Y1 and Y2 in answer choice 3 but at least we do not see e can see that there are not 2 different functions being graphed