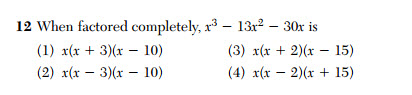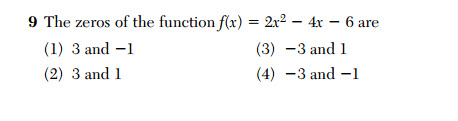From the January 2016 Common Core Algebra I Regents

This is 2 points easily earned with a TI-84 while learning about the different types of
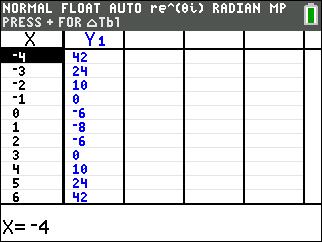
functions through comparing and contrasting.  We need to check the xy table of each function and see if it matches the given table.

Below is answer (1) not a match.  By the way, check out the change in y — linear!!

Below is answer (2) also not a match.  Check out the change in y — linear!!

Onto answer choice (3) see below, um also not a match

And last but certainly not least, answer choice (4) see below: 2 points!!!!!

There are many extensions to this question!!

Linear vs exponential vs cubic in an equation and in a table
Use the TI-84 and also look at the equations to categorize the types of functions.

Two are linear as they look like y = mx + b and will graph in a line.
One of the functions is a power function and one is exponential.

Looking at rate of change of the xy table

Substituting in values of x into each equation to see if they make the equation true
The easiest x value to substitute is usually 0 so try it here and see if the y or f(x) value = 1 as shown in the table

From the January 2016 Common Core Algebra I Regents:

p is the number of people — which must be positive leaving answers (1) and (2).
What is an integer?  Integer is related to the word integrity which means whole.
Real numbers means all numbers including non-integers like 1.5 — you cannot have 1.5 people

From the January 2016 Common Core Algebra I Regents

We can ‘do the FOIL’ or double distributive and/or we can use the TI-84 to find the equivalence to the given.  The choices look appealing as both 3 x 10 and 2 x 15 are factor pairs of 30.
To do  FOIL, we do the parentheses first in each case and then multiply by x and see if it matches the given x^3 – 13x ^2 -30x
(1) FOILing (x + 3) (x – 10) gives x^2 – 10x + 3x – 30 = x^2 -7x -30 and when  multiplied by x does not look like the original
(2) FOILing (x – 3) (x – 10) gives x^2 – 10x – 3x + 30 = x^2 -13x + 30 and when  multiplied by x does not look like the original
(3) FOILing  (x + 2) (x – 15) gives x^2 – 15x + 2x + 30 = x^2 -13x – 30 and when  multiplied by x looks familiar!
(4) FOILing (x – 2) (x + 15) gives x^2 + 15x – 2x – 30 = x^2 +13x – 30 and when  multiplied by x does not look like the original

Here is the TI-84 way — looking for equivalence :)
As you can see below answer choice (1) not a match

As you can see below answer choice (2) is also not equivalent:

Onto answer choice (3), see below: it’s a keeper –= this algebra is equivalent!!!!

From the January 2016 Common Core Algebra I Regents:

Y=, graph, table
Looking for zeros!!!
Where do you see the parabola crossing the x-axis on the graph?
For what values of x does y have a value of zero?

Look at the answers carefully — they are trying to trick us with negative signs!!

and that’s it!!  You just got 2 more points awesome!!!
PS on Parts II, II, IV you would be expected to factor this but with multiple choice

From the January 2016 Common Core Algebra I Regents
 Put 1300(1.02)^7 into the TI-84, it will come out to more than 1300!!
The money is growing  and also since 1.02 >1, the money is increasing.

So it has to be growth which is either answer 2 or 4
The exponential growth formula given on the Regents reference sheet is way complicated.
Here is a much much better one:

In our equation A = 1300 (1.02)^7
1300 is the principal or starting amount and the time = 7
The number in the parentheses is (1.02) which is equal to (1 + r)
Therefore r = .02 which is 2 cents or 2%
Now look at answers (2) and (4)
Notice that .02% growth would have the decimal .0002 as r and this is not the case.