First add y and z
y = 3x^3 + x^2 – 5 and z = x^2 – 12
What like terms do you see? Combine them — be careful of the signed integers
Then double all the terms for 2(y + z)
Category Archives: Common Core Algebra I
Get the Math and the Points Aug 2018 CC Alg I Regents #12
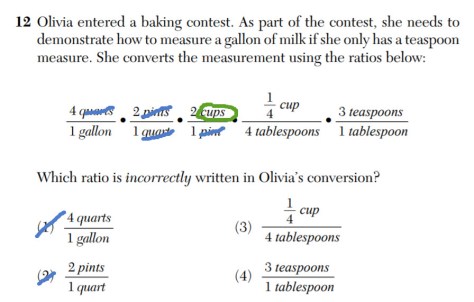
(sidenote: As a former engineer, I am not quite sure of the accuracy of Olivia’s measurement. )
This problem is a classic type of dimensional analysis exercise and two of the answers can be immediately eliminated.
Then try flipping (3) and then (4) and see which one cancels out tablespoons and cups resulting in teaspoons over gallons.
Get the Math and Points! Aug 2018 CC Alg I Regents #11
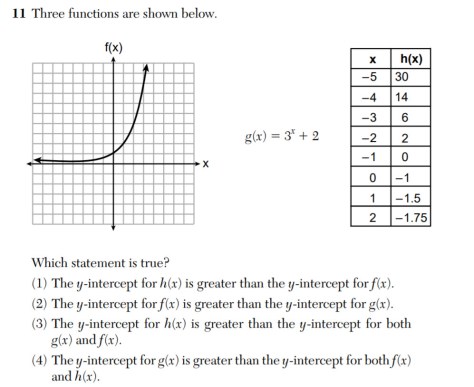
Whenever there is a y-intercept, x = 0
For f(x), where is the y-intercept? Look at the y-axis — where does it cross?
For g(x), substitute in x = 0, so g(0) = 3^0 + 2
For h(x), look at the table for when x = 0.
Then compare these y-intercepts with one another.
Which is the greatest?
Get the Math and Points Aug 2018 CC Algebra I Regents #10
This is another close reading question (like #9)
The top inequality in each answer — should it include 50? or not?
Should r be more than 10 or less than 10?
Should g include 12 or not?
Get the Math and Get the Points Aug 2018 CC Algebra I Regents #9
This is actual a close reading question. The questions to ask yourself are:
D and Q together are how many coins?
How much is D worth and how much is Q worth?
Math Confidence by Robin the Math Lady 