
Domain means x values and Range means y.
D comes before R in the alphabet and x is before y.
This problem gives us x values so use them to find y.
f(x) = 2x^2 – 8
f(-2) = 2(-2)^2 – 8 = 2(4) – 8 = 0 (This narrows it down to answers (3) or (4)!)
f(3) = 2(3)^2 – 8 = 2(9) – 8 = 10 (This makes the answer jump out at ya!)
f(5) = 2(5)^2 – 8 = 2(25) – 8 = 42
Can also use the table from the TI-84 :)
Category Archives: Regents
Get the Math and Get the Points! CC Alg I Regents Jan 2018 #1

How did 6 – 2(x^2 – 1) become 6 – 2x^2 +2?
Help Evan identify this first step of his problem solving :)
That’s it! 2 points on the Regents!

Get the Math & the Points! Jan 2018 CC Alg I Regents #6
Look for the point that does not make the equation true.
This is a very accessible question as all the x values in the choices are negative integers (-4, -3, -2, and -1) and will easily be found on the table.
When x = -4, y = -60 check
When x = -3, y = -24 check
When x = -2, y = -6 check
Um, when x = -1…
Most, if not all students, can build understanding of Math and critically think while gaining points to pass the Regents! This question from January 2018 asks the student to notice the word not and to find the point that does not belong.
2 points :)
Get the Math and the Points Jan 2018 CC Alg I #2

Two questions to ask:
1. Does V(x) grow or decay?
2. When putting 4(0.65)^x vs 4(1.35)^x into the Y= of the TI-83/4, does the table look like the one above?
Hopefully the student will know that the number in parentheses (the growth/decay factor) determines if it is growth or decay but through the graphing calculator, they can figure it out, get the right answer and earn 2 points!
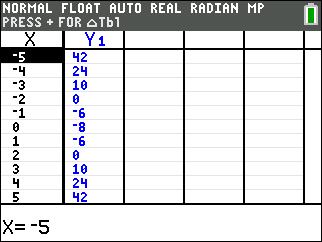
Get the Math and the Points! CC Alg I June 2017 Regents #10
 Can use the TI-83/4 to figure this one out!
Can use the TI-83/4 to figure this one out!
The zeros are the values of x that make f(x) or y equal to zero.
Answer (1) looks like this: only 1 zero at x = -3 which can be seen on both the graph and the table

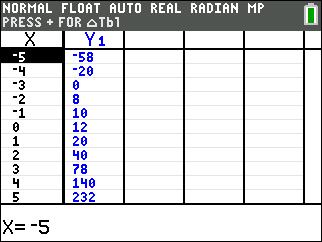
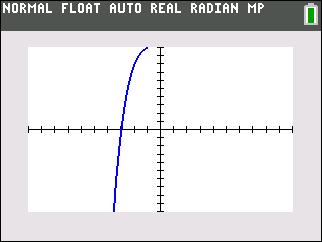
Answer (2) looks like this with 3 zeros but only one of them is an integer value (both the table and the graph show that (-4,0) is a point

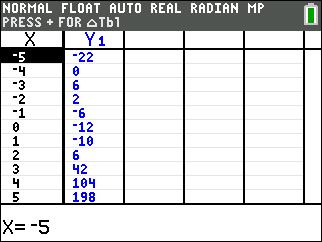
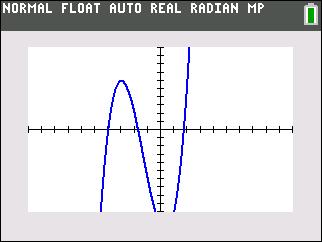
Let’s try answer (3):

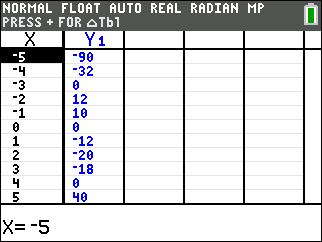
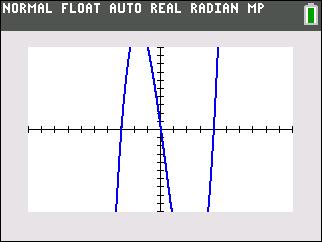
Here we can see that on the table when x = -3 y = 0 and also when x = 0 and x = 4, y is also equal to zero. Looking at the graph we can see that the 3 x-intercepts are integer values of -3, 0 and 4. That’s it!
Pay close attention to the signs!! We need to look for the factors with the opposite sign to ‘zero it out’! This can be a bit counterintuitive as when -3 is a solution then the factor is (x + 3), as -3 makes x + 3 = 0. When 4 is a solution, the factor must be (x – 4) rather than (x+4) as plugging in 4 would not result in zero.


