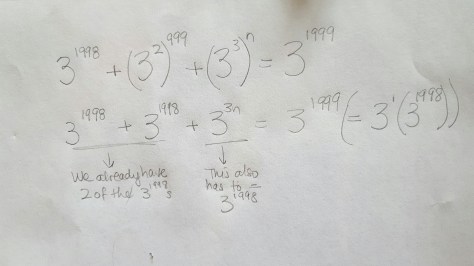Category Archives: brain puzzler

brain puzzler

March 2018 Brain Puzzler Solution

Leave a comment

Q: Leaving at 8:00 AM, if Ms. Brown drives at an average speed of 40 miles per hour, she will be late by 3 minutes. If she drives at an average speed of 60 miles per hour, she will be early by 3 minutes.  How many miles per hour does Ms. Brown need to drive to get to work exactly on time?

A: 48 miles per hour

There is a 6 minute difference between the fast (60 mph) speed and the slow (40 mph) speed.  This 6 minutes is 1/10 of an hour.
Distance = rate x time.  The two distances are equal so:
We can figure out how long it would take at 60 mph and go from there.
40 (t + .1) = 60 t
40t  + 4 = 60 t
4 = 20 t
4/20 = t = 1/5 hour
So it will take 1/5 hour at 60 mph which is 12 miles. (1/5 hour = 12 minutes)
It will take abit longer at 40 mph:
1/5 hour + 1/10 hour =
.2 hour + .1 hour = .3 hour at 40 mph  which is also 12 miles. (.3 hour is 18 minutes).
If Ms. Brown was exactly on time it would take her 15 minutes to go the 12 miles.
12 miles in 15 min = 48 mph.

brain puzzler

February 2018 Brain Puzzler Solution

Leave a comment
Q: For a calendar, with two six sided dice make all possible monthly dates using two digits  (from 01 to 31) by writing one digit (from 0, 1, 2, …, 8, 9) on each face of the two dice.
A: It does not seem like it can be done — but…the Eureka part of the answer is:
the 9 is the 6 upside and vice versa!
Dice 1: 0 1 2 4 5 7 and  Dice 2: 0 1 2 3 8 9 (9 is also 6)
or
Dice 1 : 0 1 2 3 4 5 and Dice 2 : 0 1 2 6 7 8 (6 is also 9)

brain puzzler

January 2018 Brain Puzzler Solution

Leave a comment

Q: What is the sum of the digits of the square of $111,111,111$?

A: 81
Using the standard multiplication algorithm, $111,111,111^2=12,345,678,987,654,321,$whose digit sum is 81.

Or by looking at the pattern:

$11^2 = 121 \\ 111^2 = 12321 \\ 1111^2 = 1234321$

$111,111,111^2=12,345,678,987,654,321$ whose digit sum is 81
There is a shortcut to adding these digits
Reading from left to right, we can add the first 8 digits, 1 through 8 by making 4 pairs of 9 (1 + 8, 2 + 7, 3 + 6 and 4 + 5) making 36
Reading from right to left, we can add the last 8 digits (1- 8) the same way making 36.
Leaving the middle digit of 9.

36 + 36 + 9 = 81

brain puzzler

December 2017 Brain Puzzler Solution

Leave a comment

Q: For the positive integers up to and including 2017, how many of those integers have at least one zero?

A:  There are $2017$ positive integers in total to consider.
No one digit numbers have a 0 (1-9).
Below is the list of the qualifying numbers:

There are 9 two digit numbers: 10,20, 30…90 9
There are the numbers 100 – 110 and 200-210 up to 900 – 910 99
Also 120 130 140…190 and then 220 230 etc 72
Then 1000-1099 100
Then same # of #s 1000 more than b 99
Then same # of #s 1000 more than c 72
2000-2017 18
 Total  469

Another solution is to exclude the numbers that do not have a zero and subtract from 2017:
9 one digit numbers
81 two digit numbers (9 x 9 : 9 choices for each digit 1-9)
729 three digit numbers (9 x 9 x 9: 9 choices for each digit 1-9)
For the numbers between 1000- 1999, there are the same amount as for the three digit numbers as they are the same numbers with a “1” in the thousands place value.
9 + 81 + 729 + 729 = 1548
2017 – 1548 = 469

 

 

brain puzzler

November 2017 Brain Puzzler Solution

Leave a comment

Q: I drive at an average speed of 30 miles per hour to the railroad station each morning and just catch my train. On a particular morning there was a lot of traffic and at the halfway point I found I had averaged only 15 miles per hour. How fast must I drive for the rest of the way to catch my train?

A: It’s impossible. 
Let’s say that you need to go 30 miles which would take an hour.
If you were at the halfway point, 15 miles, at 15 miles per hour, you have already been traveling for an hour  to go that 15 miles — and you are only halfway there!
Sorry…you will miss your train.